
I agree Our site saves small pieces of text information (cookies) on your device in order to deliver better content and for statistical purposes. You can disable the usage of cookies by changing the settings of your browser. By browsing our website without changing the browser settings you grant us permission to store that information on your device.
PHENOMIN offers professional assistance to tailor your prospective project to your needs. In consultation with our staff, you will have the opportunity to design the project that maximizes the value of your research.
Model Preparation |
Our panel of genetic tools and grafted models provide various starting points for analysis. |
Disease Examination / Phenotyping tests |
Your field of interest is likely already represented among our validated tests on offer. We can walk you through the specific benefits and drawbacks of tests sorted by disease involvement . |
Statistical Needs |
PHENOMIN proudly offers assistance from resident statisticians for statistical prediction based on prior testing and application of the appropriate tests |
Representative Data |
We offer representative data for each of our tests that you will know in advance how you want the analysis tailored to your question. |
Zootechny |
Various housing, archiving, and distribution capabilities are at your disposal for planning your work. We also have numerous archived lines that may be applicable to your project. |
Test Execution / Reporting |
Our project managers provide centralized and informed supervision of the tasks as they progress through PHEMOMIN, including detailed reports incorporating interpretation of our experts. |
PHENOMIN performs different statistical analysis on your phenotypic results to guarantee their validity. From basic outlier detection, up to cohort size optimisation, here are some of the analysis that are done.
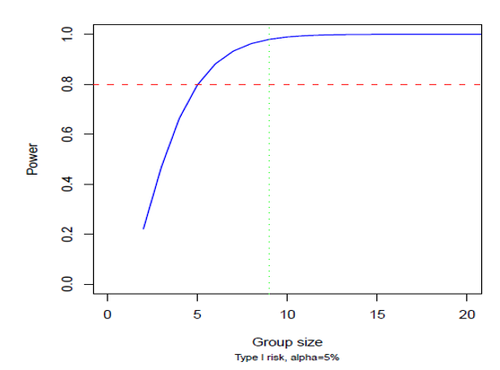
The power of a statistical test is the probability to detect a significant difference between groups if it exists.
Group size, effect size, significance level and power are linked together with mathematical relationship. In these conditions we can assess the group size necessary to get the best chances to detect significant differences between 2 groups of mice for given effect size, power and significant level.
Power is important to calculate in order to optimize experimental protocols and also to assess what we were really able to see.
We usually try to reach a power of 80-90%.
![]() Procedure to estimate the requested animal number (189.4 KB)
Procedure to estimate the requested animal number (189.4 KB)
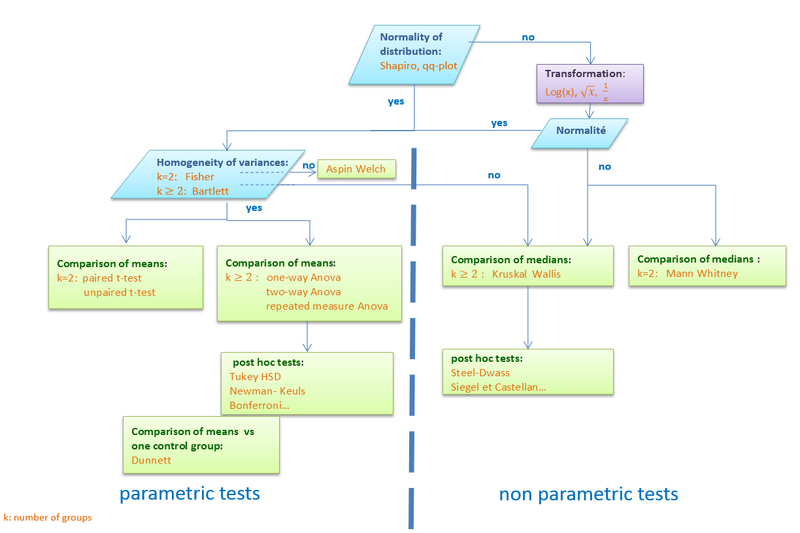
In order to perform parametric statistical tests assuming normal distribution of data, we checked the distribution of raw data and determined the transform that should be applied to get a normal distribution. For each parameter, distribution of the raw data, decimal logarithm and square root transformations were considered. We assessed normality using visual inspection of the distributions, box plots, Q-Q plots (quantile-quantile plots), and by performing the Shapiro-Wilk test.
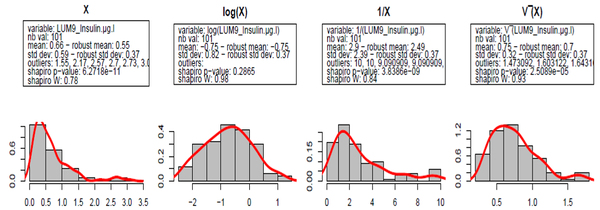
If none of these transformations allows a normal distribution, non-parametric tests should be used.
For each parameter, arithmetic mean and coefficient of variation (CV: ratio of the standard deviation (s) divided by mean, in percentages) were used as indicators of central value and variability of parameters values.
Stability across time of CV was evaluated using a χ² (khi2) goodness of fit test with a significance level of 5% to see whether the observed CV distribution follows a theoretical uniform distribution which values equal to total CV.
Stability across time of mean is evaluated using Tukey's HSD (Honestly Significant Difference) test. Each possible combination of pair of cohorts was tested. We calculated a new indicator (SCP), which is the percentage of comparisons showing a significant difference (with a significance level of 5%), reported to the total number of comparisons performed. Based on this indicator, we determined the thresholds at which we can estimate that the mean is stable or not. These thresholds were established by examining the results of the body weight parameter. For SCP below 12%, parameter’s mean is assessed stable. For SCP above 18%, parameter’s mean is assessed not stable. There is a batch effect. Stability is mixed for SCP between 13 and 17%.
For parameters with non-normal distribution, stability is assessed using a non-parametric test for multicomparisons: Kruskal Wallis.
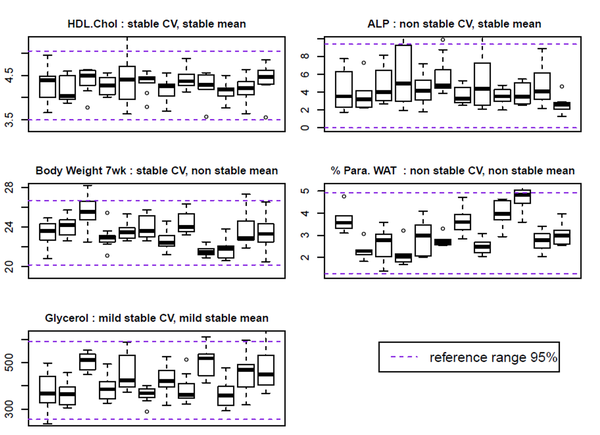
It is the interval between which a certain percentage of measured values of a reference population fall into. It allows to assess the range of physiologic values for a parameter.
About 120 experimental measures are necessary to evaluate it.
Calculation of reference range 95% (which comprises 95 % of values)
RefRange (95%) = Mean ± 2. SD
It can be used to detect phenotypes when small groups or partials groups are measured or when there is no control group to compare to. In this case we recommend to when at least 30% of values fall out of RefRange (95%).
The reproducibility of scientific results remains one of the major challenges in 21 century science, especially in our field of phenogenomics. To ensure reproducibility, each scientist must not only be an expert in its own field but master other skills that are sometimes far outside his education. For example, mathematical notions and more particularly statistics have become indispensable for good data analysis. A researcher is also required to use unfamiliar methods and technologies to answer his or her scientific question. He is expected to understand methods limits and biases for protocols that he sometimes uses for the first time.
For many years, PHENOMIN has been committed to publishing or participating in reviews and protocols focusing on technology questions. Some of these papers are based on years of data, thus allowing a great robustness of the proposed protocols.
Today, 15 papers are available in the field of the creation of genetically modified rodents and answer different technological questions:
2021
Droplet Digital PCR or Quantitative PCR for In-Depth Genomic and Functional Validation of Genetically Altered Rodents. Loic Lindner, Pauline Cayrou, Thomas W. Rosahl, Esther Heather Zhou, Marie-Christine Birling, Yann Herault, Guillaume Pavlovic. Methods, Apr 2021, S1046202321000931, doi.org/10.1016/j.ymeth.2021.04.001.
2020
Modeling Down syndrome in animals from the early stage to the 4.0 models and next. Maria Del Mar Muñiz Moreno, Véronique Brault, Marie-Christine Birling, Guillaume Pavlovic, Yann Herault. Prog Brain Res 2020 251:91-143. doi: 10.1016/bs.pbr.2019.08.001. Epub 2019 Oct 22
Variability in Genome Editing Outcomes: Challenges for Research Reproducibility and Clinical Safety. Lydia Teboul, Yann Herault, Sara Wells, Waseem Qasim, Guillaume Pavlovic. Mol Ther 2020 Jun 3;28(6):1422-1431. doi: 10.1016/j.ymthe.2020.03.015.
Reliable and robust droplet digital PCR (ddPCR) and RT-ddPCR protocols for mouse studies. Loic Lindner, Pauline Cayrou, Sylvie Jacquot, Marie-Christine Birling, Yann Herault , Guillaume Pavlovic. Methods 2020 Jul 25;S1046-2023(19)30319-6. doi: 10.1016/j.ymeth.2020.07.004.
Universal Southern blot protocol with cold or radioactive probes for the validation of alleles obtained by homologous recombination. Gemma F Codner, Valerie Erbs , Jorik Loeffler , Lauren Chessum , Adam Caulder, Nicolas Jullien, Sara Wells , Marie-Christine Birling, Lydia Teboul. Methods 2020 Jun 26;S1046-2023(20)30086-4. doi: 10.1016/j.ymeth.2020.06.011.
Conditional switching of KIF2A mutation provides new insights into cortical malformation pathogeny. Johan G Gilet, Ekaterina L Ivanova , Daria Trofimova , Gabrielle Rudolf , Hamid Meziane, Loic Broix, Nathalie Drouot , Jeremie Courraud, Valerie Skory , Paul Voulleminot, Maria Osipenko, Nadia Bahi-Buisson, Binnaz Yalcin , Marie-Christine Birling, Maria-Victoria Hinckelmann , Benjamin H Kwok, John S Allingham, Jamel Chelly. Hum Mol Genet 2020 Mar 27;29(5):766-784. doi: 10.1093/hmg/ddz316.
2019
Optimizing PCR for Mouse Genotyping: Recommendations for Reliable, Rapid, Cost Effective, Robust and Adaptable to High-Throughput Genotyping Protocol for Any Type of Mutation. Jacquot S, Chartoire N, Piguet F, Hérault Y, Pavlovic G. Curr Protoc Mouse Biol. 2019 Dec;9(4):e65. doi: 10.1002/cpmo.65.
2017
Atp6ap2 ablation in adult mice impairs viability through multiple organ deficiencies. Wendling O, Champy MF, Jaubert S, Pavlovic G, Dubos A, Lindner L, Jacobs H, Mark M, Combe R, Da Cruz IG, Luche H, Mudgett JS, Rosahl T, Sorg T, Malissen M, Reilly PT, Herault Y. Sci Rep 2017 Aug 29;7(1):9618
Modeling human disease in rodents by CRISPR/Cas9 genome editing. Birling MC, Herault Y, Pavlovic G. Mamm Genome. 2017 Jul 4.
Efficient and rapid generation of large genomic variants in rats and mice using CRISMERE. Birling MC, Schaeffer L, André P, Lindner L, Maréchal D, Ayadi A, Sorg T, Pavlovic G, Hérault Y. Sci Rep 2017 Mar 7;7:43331.
2016
Toxic gain of function from mutant FUS protein is crucial to trigger cell autonomous motor neuron loss. Scekic-Zahirovic J, Sendscheid O, El Oussini H, Jambeau M, Sun Y, Mersmann S, Wagner M, Dieterlé S, Sinniger J, Dirrig-Grosch S, Drenner K, Birling MC, Qiu J, Zhou Y, Li H, Fu XD, Rouaux C, Shelkovnikova T, Witting A, Ludolph AC, Kiefer F, Storkebaum E, et al. EMBO J. 2016 May 17;35(10):1077-97.
Aneuploidy screening of embryonic stem cell clones by metaphase karyotyping and droplet digital polymerase chain reaction. Codner GF, Lindner L, Caulder A, Wattenhofer-Donze M, Radage A, Mertz A, Eisenmann B, Mianne J, Evans EP, Beechey CV, Fray MD, Birling MC, Herault Y, Pavlovic G, Teboul L. BMC Cell Biol. 2016 Aug 5;17(1):30.
2015
Blastocyst genotyping for quality control of mouse mutant archives: an ethical and economical approach. Scavizzi F, Ryder E, Newman S, Raspa M, Gleeson D, Wardle-Jones H, Montoliu L, Fernandez A, Dessain ML, Larrigaldie V, Khorshidi Z, Vuolteenaho R, Soininen R, André P, Jacquot S, Hong Y, de Angelis MH, Ramirez-Solis R, Doe B. Transgenic Res. 2015 Oct;24(5):921-7
2014
Generation and Use of Transgenic Mice in Drug Discovery. Pavlovic, G., Brault, V., Sorg, T. and Hérault, Y. Methods And Principles In Medicinal Chemistry: In Vivo Models For Drug Discovery 2014 11 aug ; 62 (part 6):131-148
2012
Highly-efficient, fluorescent, locus directed cre and FlpO deleter mice on a pure C57BL/6N genetic background. Birling MC, Dierich A, Jacquot S, Hérault Y, Pavlovic G. Genesis. 2012 Jun;50(6):482-9.
16S rRNA gene studies (amplification of hypervariable regions of the 16S region followed by high-throughput sequencing of this PCR product) are widely performed for bacteria identification and quantification. However, many technical challenges are to be considered to ensure good quality and reproducibility of 16S sequencing and analyses. Sample storage and nucleic acid isolation methods influence the composition of the microbiome in the extracted sample. PCR and sequencing errors, filtering algorithms and methods for data analyses impact the veracity and the taxonomic resolution that can be achieved. Finally all these topics consist in the best practices for improving the reproducibility of 16S experiments.
Genome editing tools (especially CRISPR/Cas9) have already revolutionized biomedical research. But what promise do they hold for clinical studies? Several years of using genome editing in basic research have revealed the unpredictable nature and the uncertainty of the mutations that are obtained. While the bearing of off-target effects is widely known (& sometimes overestimated); on-target effects are less recognized and underestimated. Recent work from animal and cell models demonstrates the importance of extensive validation for the risk assessment of genome editing and its impact on cell integrity.
Genotyping is an essential step in animal research as it enables the selection of animals that will be bred to amplify a colony (or euthanised to control the space available in the animal house) and of course used in experimental protocols.
Wrongly, genotyping may be considered as an easy step to carry out, but providing accurate and rapid results can be more difficult than one may think. Few data are published on inconclusive genotyping, but it is believed that the classical error rate is close to 10% in mice. Lloyd et al. showed than more 15% of the lines deposited in public repositories such as the MMRRCs and Jackson Laboratory (JAX) do not carry the mutation specified by the depositor. False negative and false positive genotyping can clearly be considered as one of the many factors influencing pre-clinical studies and basic research contributing to the "reproducibility crisis".
As part of the 3Rs improvements, transgenic rodent genotyping is slowly beginning to move from biopsy sampling to different non-invasive methods, such as buccal or anal swabs, faeces or hair follicles. These protocols are rarely applied by scientists for fear of their reliability and non-repeatability and because of the risk of increased contaminations. We have evaluated different non-invasive sampling methods in order to develop a refined and more importantly a robust method that does not increase genotyping errors.
The 3 topics were presented as a learning series features from Charles River short training session during Spring 2021; you can find on-demand the presentations (each no more than 15 minutes) across six different tracks.